GMPRO docs: Solving the VRP with route clustering and soft constraints
Using GMPRO's distanceLimit and softMaxMeters fields to cluster delivery routes optimally.
The most frequent complaint I hear from clients unhappy with their route optimization algorithm is that their routes overlap. In this blog post, I'll explain how to use the distanceLimit and softMaxMeters soft constraints in the GMP Route Optimization API to create tight, high-density clusters that avoid overlap.
Part 1: GMPRO: Google Maps Platform route optimization API
Part 2: GMPRO TSP solver: Google Maps with more than 25 waypoints
Part 3: Google Maps route optimization: multi vehicle
Part 4: Fleet routing app - free Google Maps route planner for multiple stops
Part 5: GMPRO docs: Fixed vehicle costs
Part 6: GMPRO docs: Territory optimization and route planning
Part 7: GMPRO docs: Solving the VRP with route clustering and soft constraints (this article)
Part 8: GMPRO docs: Driver load balancing with soft constraints
Part 9: GMPRO docs: Driver breaks
Part 10: GMPRO docs: Complete deliveries before pickups in cargo bike logistics
Route clustering and why do routes overlap?
When a human dispatcher plans routes, the natural thing to do is to group nearby locations or stops together to form smaller, more manageable sets or "clusters." His goal is to create efficient routes by minimizing travel distance or time within each cluster, ensuring that vehicles stay within a specific area (which is one reason why territory optimization as an route planning tool is so popular). This allows drivers to easily revisit customers they missed at the beginning of their route, reducing the number of failed deliveries. Additionally, it ensures drivers can deliver in areas they are already familiar with.
A typical route optimization algorithm on the other hand, only cares about minimizing total cost or travel time, without considering other factors like route clarity or customer experience, leading to overlaps as a side effect.
If the algorithm doesn't have soft constraints (like distance limits or region boundaries) to encourage route clustering, it may optimize for overall efficiency but still allow vehicles to travel into each other's zones. Here's a Vehicle Routing Problem (VRP) example on a unit (1 km x 1 km) grid that illustrates this.
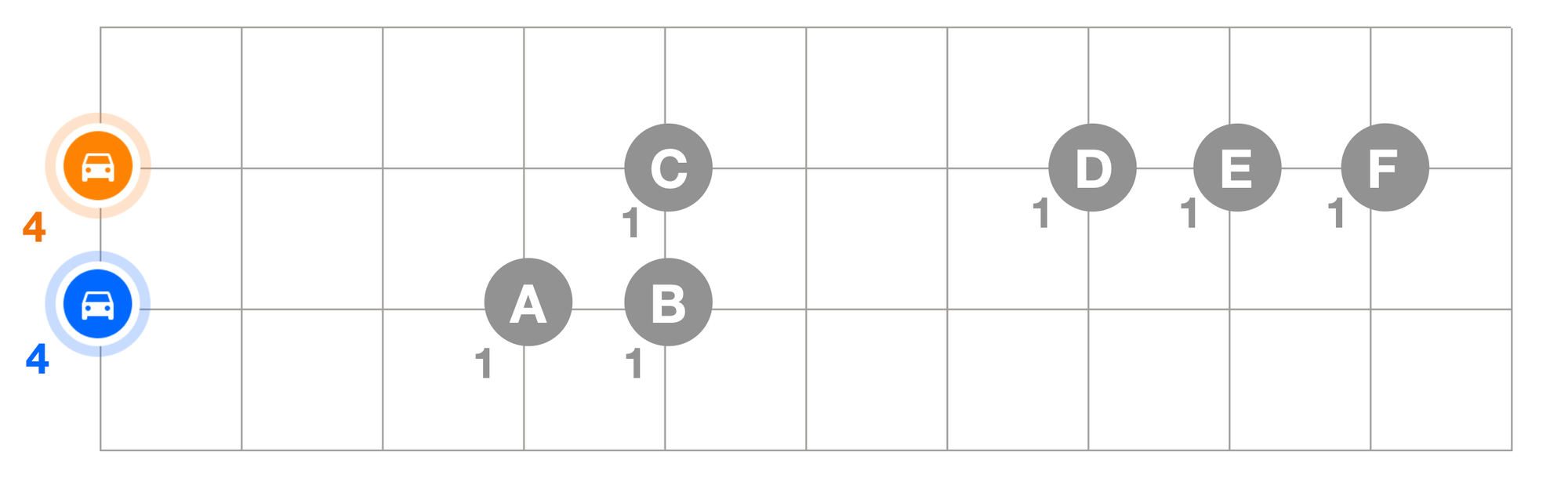
In the VRP above, we have two vehicles, orange and blue, each with a capacity (maxLoad) of 4. Together, they have to make 6 deliveries, each of load (amount) 1. What's the optimal way to make all 6 deliveries?
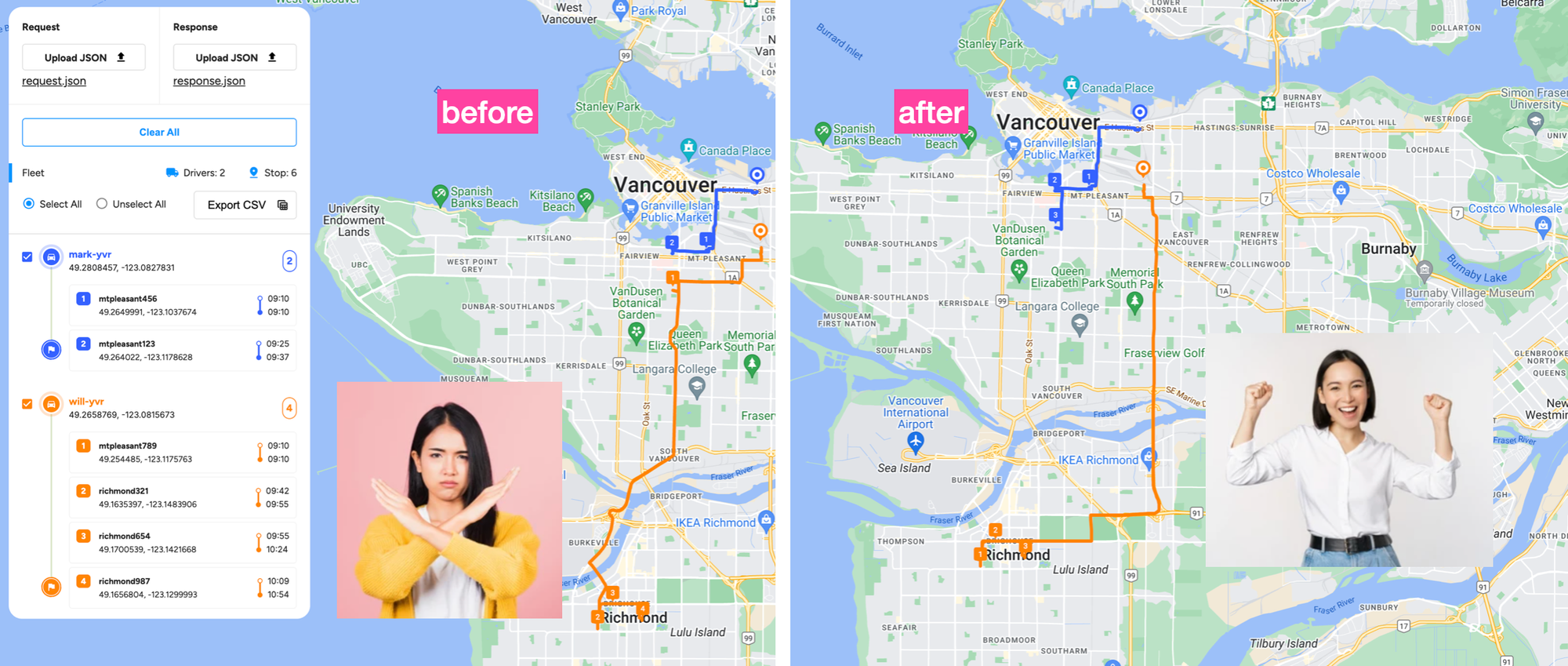
After some trial and error, you'll find that the most efficient way to solve the VRP is for the orange driver to do stops C, D, E and F and the blue driver to do A and B for a total cost of 13 i.e. 4+3+1+1 (orange) and 3 + 1 (blue). However, this does mean that the cluster made up of nearby stops A, B and C is served by two drivers. Here's a real world example of that happening:
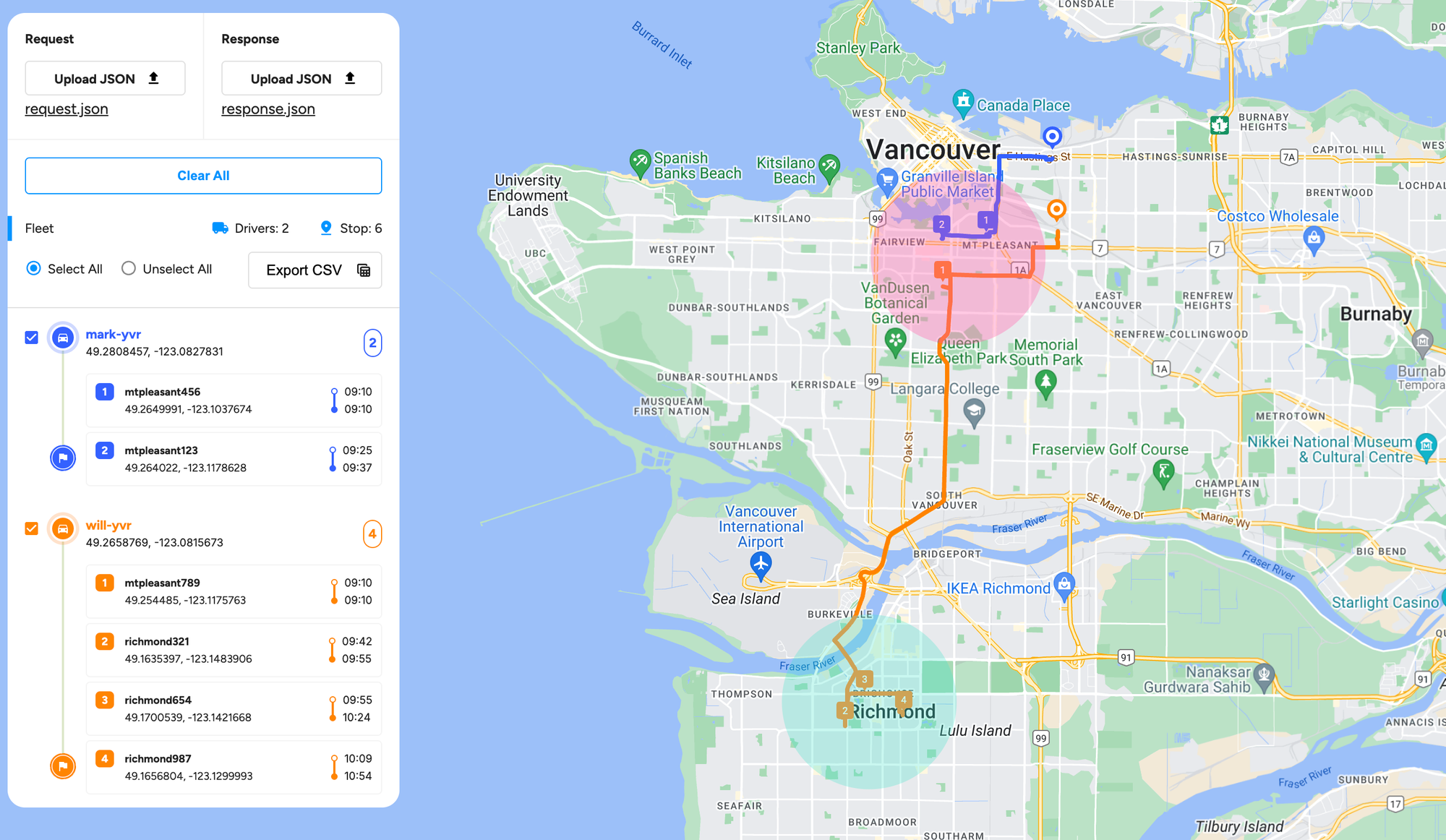
You can see that the pink cluster is served by both blue (mark-yvr) and orange (will-yvr) drivers. orange makes his first delivery in the pink cluster in the Mount Pleasant neighbourhood on his way to deliver 3 more packages in the teal cluster down south, in Richmond.
Input
{
"model": {
"shipments": [
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.264022,
"longitude": -123.1178628
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "mtpleasant123"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.2649991,
"longitude": -123.1037674
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "mtpleasant456"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.254485,
"longitude": -123.1175763
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "mtpleasant789"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.1656804,
"longitude": -123.1299993
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "richmond987"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.1700539,
"longitude": -123.1421668
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "richmond654"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.1635397,
"longitude": -123.1483906
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "richmond321"
}
],
"vehicles": [
{
"startLocation": {
"latitude": 49.2808457,
"longitude": -123.0827831
},
"loadLimits": {
"weight": {
"maxLoad": 4
}
},
"startTimeWindows": [
{
"startTime": "2024-07-08T16:00:00Z"
}
],
"endTimeWindows": [
{
"endTime": "2024-07-08T18:00:00Z"
}
],
"label": "mark-yvr",
"costPerKilometer": 1,
"startTags": ["veh-start"]
},
{
"startLocation": {
"latitude": 49.2658769,
"longitude": -123.0815673
},
"loadLimits": {
"weight": {
"maxLoad": 4
}
},
"startTimeWindows": [
{
"startTime": "2024-07-08T16:00:00Z"
}
],
"endTimeWindows": [
{
"endTime": "2024-07-08T18:00:00Z"
}
],
"label": "will-yvr",
"costPerKilometer": 1,
"startTags": ["veh-start"]
}
],
"globalStartTime": "2024-07-08T07:00:00Z",
"globalEndTime": "2024-07-09T06:59:00Z"
},
"populatePolylines": true
}
Output
{
"routes": [
{
"vehicleLabel": "mark-yvr",
"vehicleStartTime": "2024-07-08T16:00:00Z",
"vehicleEndTime": "2024-07-08T16:35:24Z",
"visits": [
{
"shipmentIndex": 1,
"startTime": "2024-07-08T16:10:52Z",
"detour": "0s",
"shipmentLabel": "mtpleasant456",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"startTime": "2024-07-08T16:25:24Z",
"detour": "768s",
"shipmentLabel": "mtpleasant123",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
}
],
"transitions": [
{
"travelDuration": "652s",
"travelDistanceMeters": 3390,
"waitDuration": "0s",
"totalDuration": "652s",
"startTime": "2024-07-08T16:00:00Z",
"vehicleLoads": {
"weight": {
"amount": "2"
}
}
},
{
"travelDuration": "272s",
"travelDistanceMeters": 1288,
"waitDuration": "0s",
"totalDuration": "272s",
"startTime": "2024-07-08T16:20:52Z",
"vehicleLoads": {
"weight": {
"amount": "1"
}
}
},
{
"travelDuration": "0s",
"waitDuration": "0s",
"totalDuration": "0s",
"startTime": "2024-07-08T16:35:24Z",
"vehicleLoads": {
"weight": {}
}
}
],
"routePolyline": {
"points": "_dxkHnrfnV?`@HAN??f@Ar@@^@TDPFRBP@F?@@P?^?^?X?BAp@eBCATGxL?\\GlMAHChGAhBEfKAbD?BAt@A`DGfLCxGCtB?`@tABjABZ?vCF\\@xA?tA@x@Bh@NrADJ?J@f@?rBFF?D@bCBhCDlA@T@jCFtA@dDD^Bf@?R@l@@L@P@JBH@?@t@VRHLDl@Xh@TXHF@HDL@L@X@X@H?XALAP?D?`@@l@?j@@@?r@BZ?v@@jBBrA?D?FADCJG~@BlCBDF@@?@@@@?@@Z@b@@Z@j@?NBR?`@B?b@Av@?P?TAH?NAz@CbD|ADAjB?NAp@@q@?O@kBjABJ@AxF?NApBAZ?rAAv@?`ACxC?XAtA?j@?N?XAj@Av@AxA@FCrB?P?H?`@C|FG`KAtBAxAAb@?RAXC^CZG\\Cb@AL?NAN?ZAf@CzEAjDL@T@b@@L@H@D?J?d@@N@AdA"
},
"metrics": {
"performedShipmentCount": 2,
"travelDuration": "924s",
"waitDuration": "0s",
"delayDuration": "0s",
"breakDuration": "0s",
"visitDuration": "1200s",
"totalDuration": "2124s",
"travelDistanceMeters": 4678,
"maxLoads": {
"weight": {
"amount": "2"
}
}
},
"routeCosts": {
"model.vehicles.cost_per_kilometer": 4.678
},
"routeTotalCost": 4.678
},
{
"vehicleIndex": 1,
"vehicleLabel": "will-yvr",
"vehicleStartTime": "2024-07-08T16:00:00Z",
"vehicleEndTime": "2024-07-08T17:19:45Z",
"visits": [
{
"shipmentIndex": 2,
"startTime": "2024-07-08T16:10:42Z",
"detour": "0s",
"shipmentLabel": "mtpleasant789",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"shipmentIndex": 5,
"startTime": "2024-07-08T16:42:09Z",
"detour": "802s",
"shipmentLabel": "richmond321",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"shipmentIndex": 4,
"startTime": "2024-07-08T16:55:54Z",
"detour": "1753s",
"shipmentLabel": "richmond654",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"shipmentIndex": 3,
"startTime": "2024-07-08T17:09:45Z",
"detour": "2732s",
"shipmentLabel": "richmond987",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
}
],
"transitions": [
{
"travelDuration": "642s",
"travelDistanceMeters": 3973,
"waitDuration": "0s",
"totalDuration": "642s",
"startTime": "2024-07-08T16:00:00Z",
"vehicleLoads": {
"weight": {
"amount": "4"
}
}
},
{
"travelDuration": "1287s",
"travelDistanceMeters": 12134,
"waitDuration": "0s",
"totalDuration": "1287s",
"startTime": "2024-07-08T16:20:42Z",
"vehicleLoads": {
"weight": {
"amount": "3"
}
}
},
{
"travelDuration": "225s",
"travelDistanceMeters": 1388,
"waitDuration": "0s",
"totalDuration": "225s",
"startTime": "2024-07-08T16:52:09Z",
"vehicleLoads": {
"weight": {
"amount": "2"
}
}
},
{
"travelDuration": "231s",
"travelDistanceMeters": 1371,
"waitDuration": "0s",
"totalDuration": "231s",
"startTime": "2024-07-08T17:05:54Z",
"vehicleLoads": {
"weight": {
"amount": "1"
}
}
},
{
"travelDuration": "0s",
"waitDuration": "0s",
"totalDuration": "0s",
"startTime": "2024-07-08T17:19:45Z",
"vehicleLoads": {
"weight": {}
}
}
],
"routePolyline": {
"points": "qfukHjifnVxA@`@@nDI?@?@?@?@@??@?@?@@??@?@@??@@??@@?@??@@?@??A@?@??A@??A@A?A@??A?A?A?A?Ab@?h@@l@?n@@xA@z@@@?`@?AdK?r@CnI?`@?J?f@?fAA^?l@@hAKZ?@?@Af@?vA?tB?jB?jAP@zA@JADA@?bA@zAAP@x@?H@zA@|A?xA@@?vA@zA@rA@VDR@Z@@@DBFBBBNHDBNHTJb@`@f@b@VPVBXD?j@CzA?bAAv@?JA`BAnAAlC?n@AtBC`D?x@CxAAjA?dAAxA?xB?bB?dDClB?zAAbC?lB?h@@hAApA?fA?LCfFAzDAvCAl@CxCEtE?V?RGvFGrFC`EAfBAbCAbCCfCEpEA^APAr@?t@?b@|@?hC?ZGtCDN?J@tBBt@@Kr@_@jB?V?PCnGBoG?Q?W^kBJs@F?~@@vBBB?N@lB@N@J?H@J@P?r@@hBBL?fABb@?F@dBB^?lABPBD@J@D@HBXBTHF?N@tDVL@zDFf@@lCB\\?P?b@?T?DBNBF?NBD?V@LDD@D@D@FBVNf@`@@@ZXd@j@Zb@DFXh@FLVf@Vh@JTFLHLJNFJPTRRLNFDJJHFLHHDFBFBFDFBJDJBLBLBN@N@H?b@@dCFpABr@AF?D?JALCJEJEJIJKjAqAx@_ANSp@w@hAsAHIX]TUPSDEBEDGHEFGNGJEB?z@CpCDJ?v@@x@@zABz@BnA@P?l@@b@@dA@^@T?^@n@@n@BX@V?V@X@d@DrA@^?p@@jBBtBBV@h@?zABr@@N?TAl@@L?J@rA@`@@L?fA@~@@F?H@b@?T?~@@\\@t@@x@@R?xAHP?hAB~@@b@@V@V?b@@l@@V?b@@fA@L?x@@T@r@?dABlA@`A@x@@J?fADt@@N@hA@rBB|@@L?`CBrCD^?x@@jDDJ?P?fABT?p@@L?Z@N@fCD\\@b@?b@@R@fA@P@J?l@?|@@~@?~AFpABvADvADb@ARBpA@ZBPAJB@?d@CNAXz@\\`Ab@nA~@jCPV`@nA\\`Ab@tATv@Fl@^fAj@hBNb@Rj@FNr@`CNf@Pl@Ld@N`@Nh@?@Vv@^fAh@fBJRRp@JVPf@p@zBdAjDb@vAPj@Rt@XlADNJ^Tx@HVJZv@lBDJ@BFRFPBFV~@\\nBHHDHBJHTRx@X|@X~@x@hC^fAFNTj@HTJR?@R\\Vb@PRVZJHLLXT@@@?VPLFLFXJPFPDJDHBJBb@Lf@NLDLJlAZlAZfBf@`@LHBf@N`@JdAZPFtA`@fBf@hA\\HBl@RRDd@Rf@VXP\\T\\^RTPRDDFHRXPVLVLRNZJTN`@L\\Pf@HZDNFXFXBJRzAJr@?FDVBP?BDb@CVE`@It@OvAEN?BMdACJ?HCT?BALAR?T?P@P@PBRDTDPFPHNHNLTJLLJPJJDJDL@L@N?LALCLCJGHGNMNONOJOBGLQHQLQJIRSDERUBCDCLILGLGHADA@AJANAB?NAV?B?F?D?f@Bp@@N@P?rA@P@J@T@d@DTDTFXJTF`@Nj@Xb@Rl@ZjAh@l@THDJ@j@VhB|@hBx@r@XTJVLRJHDBB~C~Ah@`@^ZNNZXh@n@\\`@j@t@n@z@Z`@z@hANRRVLPV\\NRd@n@TZ`C`DXb@t@lAj@jAZf@f@`Az@zAlApBV^NTLPRa@~@mA\\e@DGd@k@@CV[@?LUf@k@h@u@LUDG@E|AiBvAaB\\a@`BkBx@aAPSFIJKBEPSTWLOPKRSZ[TUHIz@_APQJKRWb@g@RWBC\\]\\YRQRKTKPGRGNCLCLAF?F?LA^BX@B@RB\\Nj@TBBj@`@PNp@h@d@\\FFNNzBbBtBdBB@\\XJHj@`@PJNHPFNBNBJ?B?dD@P?d@@n@?n@@r@?^AP@NKfA@z@?bB?xCDZ?^?~@?P?RA?`D?l@?L@b@@X@L@JBVBJ@JBLDLDN?@JXLZFLHNfBoCSg@GOCIAKCIAIAKAS?I?C?C?K@G?C?C@G@C@A@C?ABA@ABAB?H?bCAL?vD?wD?M?cC@I?C?C@A@C@?@ABA@ABAF?B?BAF?J?B?B?H@R@J@HBH@JBHFNRf@gBnCIOGMM[KY?AEOEMCMAKCKCWAKAMAYAc@?M?m@?aDS@Q?_A?_@?[?yCEcB?{@?gAAMIWEG?S@s@Ao@Ao@?e@AA_EAc@Gc@?S?wDAgC?e@?yA?oA?qA?a@?]HY?aA?M?[?wD?}D?a@A{I?e@As@AmC?yBB_@?u@?s@?}C?q@GY?q@?c@AaA?CH{@?_A@iA?{C@mCLAtAAV?H?B?D?BAlA@B?\\AnA@Z?X@@?B?tB?H?H?L?J?L?B?N?H?j@?z@?P@@u@?q@@eDdA?d@@D?@Ah@?"
},
"metrics": {
"performedShipmentCount": 4,
"travelDuration": "2385s",
"waitDuration": "0s",
"delayDuration": "0s",
"breakDuration": "0s",
"visitDuration": "2400s",
"totalDuration": "4785s",
"travelDistanceMeters": 18866,
"maxLoads": {
"weight": {
"amount": "4"
}
}
},
"routeCosts": {
"model.vehicles.cost_per_kilometer": 18.866
},
"routeTotalCost": 18.866
}
],
"metrics": {
"aggregatedRouteMetrics": {
"performedShipmentCount": 6,
"travelDuration": "3309s",
"waitDuration": "0s",
"delayDuration": "0s",
"breakDuration": "0s",
"visitDuration": "3600s",
"totalDuration": "6909s",
"travelDistanceMeters": 23544,
"maxLoads": {
"weight": {
"amount": "4"
}
}
},
"usedVehicleCount": 2,
"earliestVehicleStartTime": "2024-07-08T16:00:00Z",
"latestVehicleEndTime": "2024-07-08T17:19:45Z",
"totalCost": 23.544,
"costs": {
"model.vehicles.cost_per_kilometer": 23.544
}
}
}
How to use soft constraints to encourage route clustering in GMPRO
The first thing we need to do is modify the objective function in the GMPRO algorithm to balance the original goal of minimizing total driving distance with new clustering constraints. The easiest way to do this is by introducing penalties if the distance travelled between consecutive stops exceeds some value.
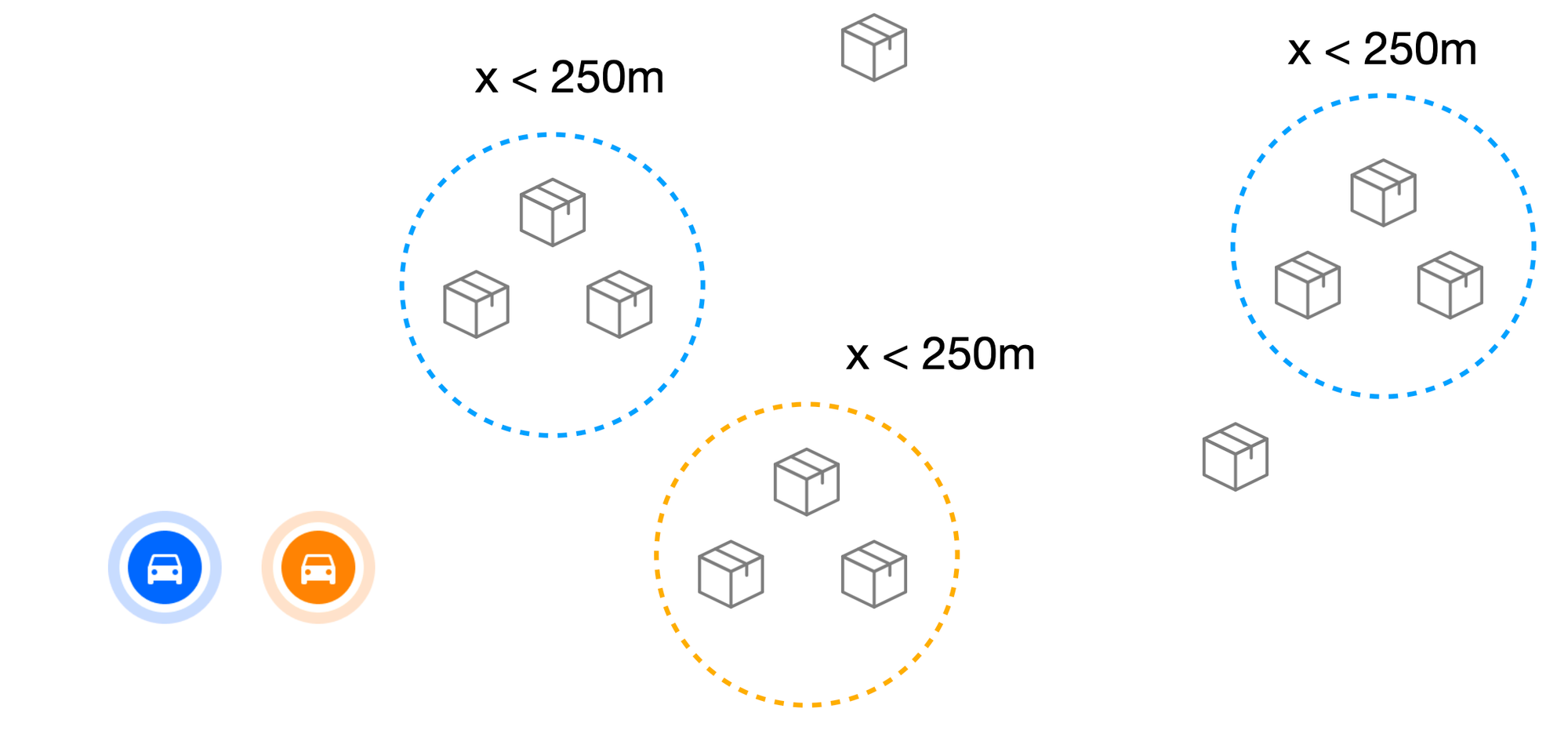
How does this work in practice? Let's say x represents the distance between two consecutive stops on a driver’s route. If x is less than a certain threshold, say 250 meters, we group those stops together by making travel within the cluster inexpensive and travel outside the cluster costly. With this approach, as shown in the image above, nearby deliveries are automatically grouped into distinct regions. This differs from territory optimization, where clusters are predefined in advance
The next step is to exclude the penalty when a driver travels from their starting location to the first stop. This ensures that if the first driver 'claims' a nearby cluster, the second driver skips stops in that cluster and moves on to the next one. Here’s an example to demonstrate how this works.
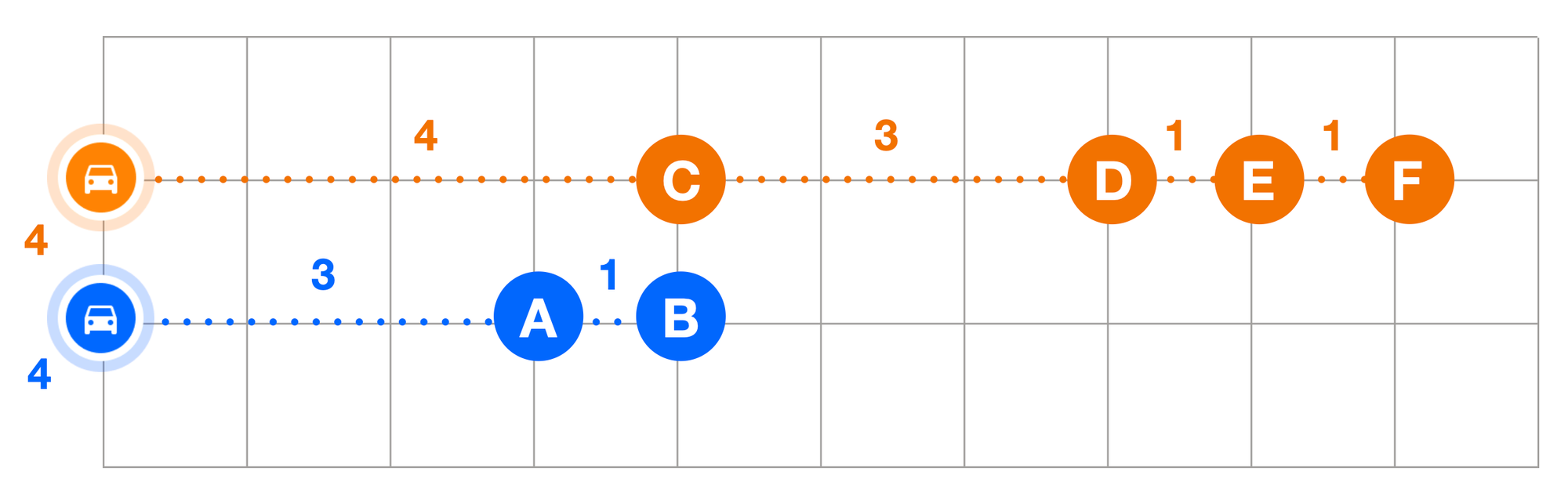
In the same VRP introduced earlier, we'll assign a travel cost of 1 when a vehicle travels between adjacent stops, and a unit travel cost of 10 when traveling between stops more than one grid apart (ignoring the travel distance to the first stop). Here’s what the optimal route solution looks like:
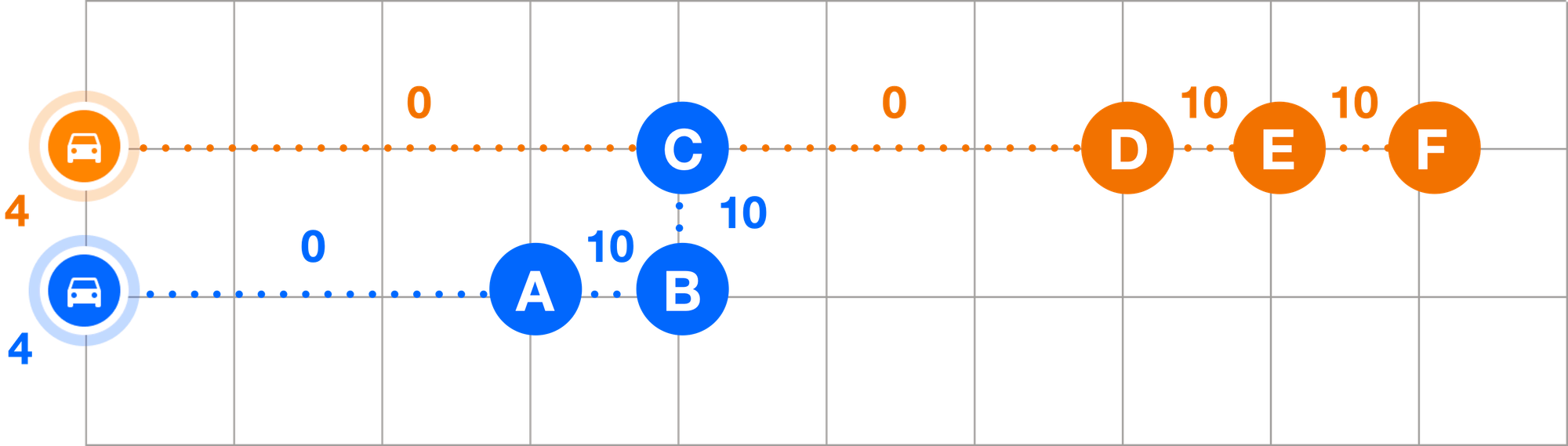
Now, the most efficient way to solve the VRP is for the orange driver to do stops D, E and F and the blue driver to do A, B and C for a total cost of 4 i.e. 0 + 1 + 1 (orange) and 0 + 1 + 1 (blue). Now, what happens if don't ignore the penalty of 10 per grid when travelling to the first stop?
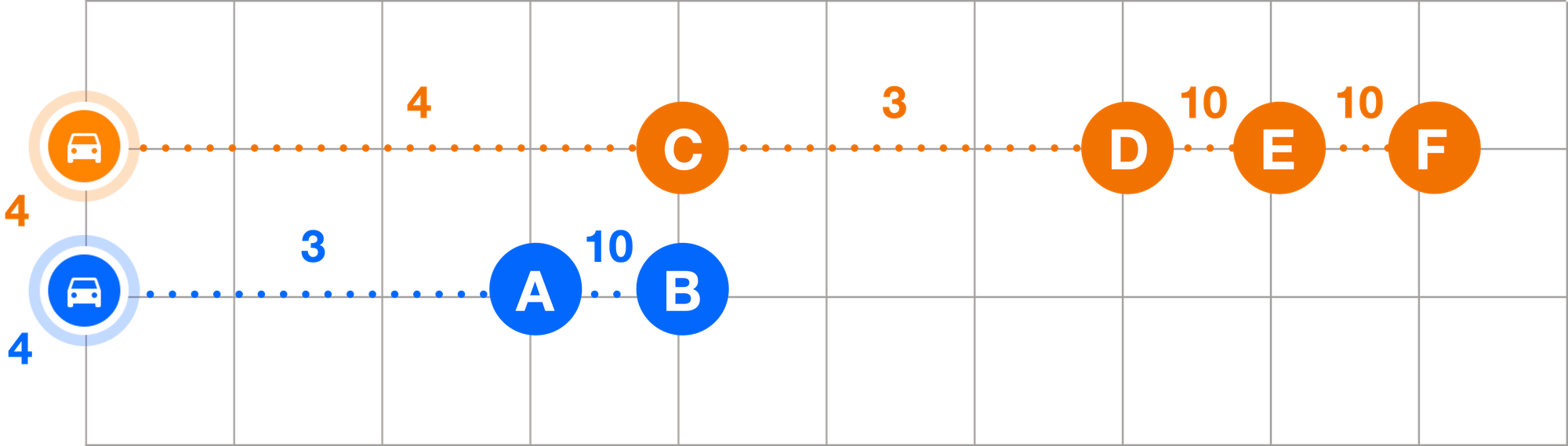
The route solution reverts to orange doing stops C, D, E and F and blue, A and B (for a total cost of 103), because stop C was on the way for the orange driver. If C was given to blue, the total cost would be 104 (an additional cost of 1 from B to C).
Building soft constraints into the GMPRO objective function
Modifying the objective function directly to incorporate penalties for crossing cluster boundaries or exceeding the distance limit for consecutive stops is surprisingly easy in GMPRO. In the model of your request, add:
{
"transitionAttributes": [
{
"excludedSrcTag": "veh-start",
"excludedDstTag": "whatever",
"distanceLimit": {
"softMaxMeters": 250,
"costPerKilometerBelowSoftMax": 1,
"costPerKilometerAboveSoftMax": 1000000
}
}
]
}and in your vehicle object, include:
{
"startTags": [
"veh-start"
]
}The JSON above defines a set of rules for transitions (vehicle travel) between stops in the GMPRO route optimization algorithm.
excludedSrcTag: "veh-start": This excludes any transitions that start from a stop tagged as "veh-start", meaning these rules do not apply when the vehicle is leaving its starting point.
distanceLimit: This defines limits and costs associated with the distance between stops.
softMaxMeters:250: This sets a soft limit of 250 meters for the distance between consecutive stops.costPerKilometerBelowSoftMax:1: If the distance between stops is within 250 meters, the cost per kilometer is 1 unit.costPerKilometerAboveSoftMax:1,000,000: If the distance exceeds 250 meters, a very high cost (1,000,000 units per kilometer) is applied to discourage such transitions (obligatory Austin Powers clip).
Here's the full worked example:
Input
{
"model": {
"shipments": [
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.264022,
"longitude": -123.1178628
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "mtpleasant123"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.2649991,
"longitude": -123.1037674
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "mtpleasant456"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.254485,
"longitude": -123.1175763
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "mtpleasant789"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.1656804,
"longitude": -123.1299993
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "richmond987"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.1700539,
"longitude": -123.1421668
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "richmond654"
},
{
"deliveries": [
{
"arrivalLocation": {
"latitude": 49.1635397,
"longitude": -123.1483906
},
"duration": "600s",
"timeWindows": [
{
"startTime": "2024-07-08T16:00:00Z",
"endTime": "2024-07-08T18:00:00Z"
}
]
}
],
"loadDemands": {
"weight": {
"amount": "1"
}
},
"label": "richmond321"
}
],
"vehicles": [
{
"startLocation": {
"latitude": 49.2808457,
"longitude": -123.0827831
},
"loadLimits": {
"weight": {
"maxLoad": 4
}
},
"startTimeWindows": [
{
"startTime": "2024-07-08T16:00:00Z"
}
],
"endTimeWindows": [
{
"endTime": "2024-07-08T18:00:00Z"
}
],
"label": "mark-yvr",
"costPerKilometer": 1,
"startTags": ["veh-start"]
},
{
"startLocation": {
"latitude": 49.2658769,
"longitude": -123.0815673
},
"loadLimits": {
"weight": {
"maxLoad": 4
}
},
"startTimeWindows": [
{
"startTime": "2024-07-08T16:00:00Z"
}
],
"endTimeWindows": [
{
"endTime": "2024-07-08T18:00:00Z"
}
],
"label": "will-yvr",
"costPerKilometer": 1,
"startTags": ["veh-start"]
}
],
"transitionAttributes": [
{
"excludedSrcTag": "veh-start",
"excludedDstTag": "whatever",
"distanceLimit": {
"softMaxMeters": 250,
"costPerKilometerBelowSoftMax": 1,
"costPerKilometerAboveSoftMax": 1000000
}
}
],
"globalStartTime": "2024-07-08T07:00:00Z",
"globalEndTime": "2024-07-09T06:59:00Z"
},
"populatePolylines": true
}
Output
{
"routes": [
{
"vehicleLabel": "mark-yvr",
"vehicleStartTime": "2024-07-08T16:00:00Z",
"vehicleEndTime": "2024-07-08T16:50:53Z",
"visits": [
{
"shipmentIndex": 1,
"startTime": "2024-07-08T16:10:52Z",
"detour": "0s",
"shipmentLabel": "mtpleasant456",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"startTime": "2024-07-08T16:25:24Z",
"detour": "768s",
"shipmentLabel": "mtpleasant123",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"shipmentIndex": 2,
"startTime": "2024-07-08T16:40:53Z",
"detour": "1506s",
"shipmentLabel": "mtpleasant789",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
}
],
"transitions": [
{
"travelDuration": "652s",
"travelDistanceMeters": 3390,
"waitDuration": "0s",
"totalDuration": "652s",
"startTime": "2024-07-08T16:00:00Z",
"vehicleLoads": {
"weight": {
"amount": "3"
}
}
},
{
"travelDuration": "272s",
"travelDistanceMeters": 1288,
"waitDuration": "0s",
"totalDuration": "272s",
"startTime": "2024-07-08T16:20:52Z",
"vehicleLoads": {
"weight": {
"amount": "2"
}
}
},
{
"travelDuration": "329s",
"travelDistanceMeters": 1508,
"waitDuration": "0s",
"totalDuration": "329s",
"startTime": "2024-07-08T16:35:24Z",
"vehicleLoads": {
"weight": {
"amount": "1"
}
}
},
{
"travelDuration": "0s",
"waitDuration": "0s",
"totalDuration": "0s",
"startTime": "2024-07-08T16:50:53Z",
"vehicleLoads": {
"weight": {}
}
}
],
"routePolyline": {
"points": "_dxkHnrfnV?`@HAN??f@Ar@@^@TDPFRBP@F?@@P?^?^?X?BAp@eBCATGxL?\\GlMAHChGAhBEfKAbD?BAt@A`DGfLCxGCtB?`@tABjABZ?vCF\\@xA?tA@x@Bh@NrADJ?J@f@?rBFF?D@bCBhCDlA@T@jCFtA@dDD^Bf@?R@l@@L@P@JBH@?@t@VRHLDl@Xh@TXHF@HDL@L@X@X@H?XALAP?D?`@@l@?j@@@?r@BZ?v@@jBBrA?D?FADCJG~@BlCBDF@@?@@@@?@@Z@b@@Z@j@?NBR?`@B?b@Av@?P?TAH?NAz@CbD|ADAjB?NAp@@q@?O@kBjABJ@AxF?NApBAZ?rAAv@?`ACxC?XAtA?j@?N?XAj@Av@AxA@FCrB?P?H?`@C|FG`KAtBAxAAb@?RAXC^CZG\\Cb@AL?NAN?ZAf@CzEAjDL@T@b@@L@H@D?J?d@@N@AdA@eADwKBaA?I@G?E@GLCFAH?rADp@@T@b@@r@?|ABl@BJ?vADX@bA?n@?L@x@?PAB@B?B?xC?NCpCD`@HJ@`@@d@@D?v@At@?jA@v@?|@?hC?ZGtCDN?J@tBBt@@Kr@_@jB?V?PCnG"
},
"metrics": {
"performedShipmentCount": 3,
"travelDuration": "1253s",
"waitDuration": "0s",
"delayDuration": "0s",
"breakDuration": "0s",
"visitDuration": "1800s",
"totalDuration": "3053s",
"travelDistanceMeters": 6186,
"maxLoads": {
"weight": {
"amount": "3"
}
}
},
"routeCosts": {
"model.transition_attributes": 2296000.5,
"model.vehicles.cost_per_kilometer": 6.186
},
"routeTotalCost": 2296006.686
},
{
"vehicleIndex": 1,
"vehicleLabel": "will-yvr",
"vehicleStartTime": "2024-07-08T16:00:00Z",
"vehicleEndTime": "2024-07-08T17:06:23Z",
"visits": [
{
"shipmentIndex": 5,
"startTime": "2024-07-08T16:28:47Z",
"detour": "0s",
"shipmentLabel": "richmond321",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"shipmentIndex": 4,
"startTime": "2024-07-08T16:42:32Z",
"detour": "951s",
"shipmentLabel": "richmond654",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
},
{
"shipmentIndex": 3,
"startTime": "2024-07-08T16:56:23Z",
"detour": "1930s",
"shipmentLabel": "richmond987",
"loadDemands": {
"weight": {
"amount": "-1"
}
}
}
],
"transitions": [
{
"travelDuration": "1727s",
"travelDistanceMeters": 17190,
"waitDuration": "0s",
"totalDuration": "1727s",
"startTime": "2024-07-08T16:00:00Z",
"vehicleLoads": {
"weight": {
"amount": "3"
}
}
},
{
"travelDuration": "225s",
"travelDistanceMeters": 1388,
"waitDuration": "0s",
"totalDuration": "225s",
"startTime": "2024-07-08T16:38:47Z",
"vehicleLoads": {
"weight": {
"amount": "2"
}
}
},
{
"travelDuration": "231s",
"travelDistanceMeters": 1371,
"waitDuration": "0s",
"totalDuration": "231s",
"startTime": "2024-07-08T16:52:32Z",
"vehicleLoads": {
"weight": {
"amount": "1"
}
}
},
{
"travelDuration": "0s",
"waitDuration": "0s",
"totalDuration": "0s",
"startTime": "2024-07-08T17:06:23Z",
"vehicleLoads": {
"weight": {}
}
}
],
"routePolyline": {
"points": "qfukHjifnVxA@`@@nDI?@?@?@?@@??@?@?@@??@?@@??@@??@@?@??@@?@??A@?@??A@??A@A?A@??A?A?A?A?Ab@?h@@l@?n@@xA@z@@@?`@?BaE?s@@s@Fe@@y@@kA?qA@_EtA@B?`@@R?\\?B@DAF?hAAX?B?p@AL?NAhAC`@@n@?J?tA@d@?t@?h@?J?FAFADAJEHCHCHEBAFGNMFGFGR[Ti@@CHUFUJ[JUDILSHMNO@AXSPG@AHCFALAJAb@A\\@n@@d@?t@BH?V?F?Z?NBb@?L?j@@b@@H?`@@HAP@^?^@H?b@@t@@l@@l@@R?dAArABpA@LAn@@f@?x@B`@@N?b@@~@@X@b@@b@@^@lA@d@?rABP@J@fA@J?H?xABx@@FCNIZ?dBBzDDF?HAfDDfC@h@@|BBfABP?P?dCBJARNz@@`BAB?h@@tA?b@@R@V@h@BH@j@DXFB?@?NGF@RDXDF@b@HNBj@H`@HD?nAJD?L@p@@P@F@D@L?x@BPAd@@V?NAt@@b@@@?b@?rDDB?fABnA@ZPh@@b@@hA@hABR?lFFl@Gb@AtA@X?tA@bABnCBPAt@@x@@jCDt@@Z?F@fA@LBHBFBHBB?\\Bj@BXB\\@h@@J?fA?P@jAB`B?LAH?HAJELChCD~HLd@?x@?lA?dB@XANANCNEDARGVI`@QLJd@OVGRCPC@?L?J?jA?fAAP?f@?`@?zA?^Gt@@vA?~A?tA@rA?b@@@?`@?N@rA?xA@jD?r@@xAAFF@?LBR@hB?fAB`A@J?Z?ZBbCFh@BN?F@D?fAB@?fABvBFF?L@L?jBDnAD|BD^@j@@^@F?d@@P?V?xABl@?Z?B?|A?`@?T?x@?B?fA?t@?P?Z?dA?H?b@?dA?d@?rA?hAAn@?r@?`@?~@?jA?b@?`@?x@?tA?R?hA?~B?Z?`@?f@ApA?`A?dB?nA?^?N?l@?v@?X?h@?T?l@?l@?X?t@?b@?Z?D?X?N?X?D?f@?XAV?j@?z@?pA?f@?n@?|A?P?lA?xA?^Av@?dB?d@?bD?T?Z?Z?^Ap@?\\AB?RATAp@ELA`@ETEVCTEVETEl@OTGVGTGTITIVITIj@U^Qn@[TMfAk@ZSx@c@BA~A}@PHRIt@_@JEnAk@~@_@r@Sn@OLB@?ZCNALA\\A@?H?H?J?F@J@J@RBTFLBFDLFJDHDHFHFHHNLLLLNNVJNBFDFFNDJBDBFDLDJBLDNBJDRH\\BL@PD^Dl@@R@R?L@L@vA?H@`C?l@@|A?V?@?@?@?@HRA`A?xA?j@?n@?R?hE?x@?f@?T@dB?n@@b@?p@B~A@\\BfA@j@B|@@~@F~B@l@@z@BdA@j@DrBD|A@z@@N@x@@d@@P@r@@f@@l@@^@h@?R@f@@r@?Z@n@?h@@pA@n@?Z?v@?`B?F?B?\\?b@?@?P?jA?l@A~B?~@AxAAzB?n@?`E?r@?t@?r@?@?Z?nAAtC?@AfI?ZC~B?lA@l@?t@?V?^VB^FR?@@^@Z@R?RALAN?VEd@IzABT@xDEb@ArBAbB?lAAtFAnC?z@?l@??lFAvY?bV?bCAjF?fC?dJ?jE?|H?l@AdRFjD?P?@@l@@d@?b@@tA?^?f@AhGG~Y?pAA~@?pAAjE?~AAfA?~@Fz@?B@`A?b@?p@IX?`CA`C?v@C\\@pB?J?~AB~A@v@?n@?jC?jC?`@?zE?vB?fA?dAFX?\\?`@?pA?nA?xA?d@@fC?vD?RG^Ah@@t@?tB@P?ZP?d@@n@?n@@r@?^AP@NKfA@z@?bB?xCDZ?^?~@?P?RA?`D?l@?L@b@@X@L@JBVBJ@JBLDLDN?@JXLZFLHNfBoCSg@GOCIAKCIAIAKAS?I?C?C?K@G?C?C@G@C@A@C?ABA@ABAB?H?bCAL?vD?wD?M?cC@I?C?C@A@C@?@ABA@ABAF?B?BAF?J?B?B?H@R@J@HBH@JBHFNRf@gBnCIOGMM[KY?AEOEMCMAKCKCWAKAMAYAc@?M?m@?aDS@Q?_A?_@?[?yCEcB?{@?gAAMIWEG?S@s@Ao@Ao@?e@AA_EAc@Gc@?S?wDAgC?e@?yA?oA?qA?a@?]HY?aA?M?[?wD?}D?a@A{I?e@As@AmC?yBB_@?u@?s@?}C?q@GY?q@?c@AaA?CH{@?_A@iA?{C@mCLAtAAV?H?B?D?BAlA@B?\\AnA@Z?X@@?B?tB?H?H?L?J?L?B?N?H?j@?z@?P@@u@?q@@eDdA?d@@D?@Ah@?"
},
"metrics": {
"performedShipmentCount": 3,
"travelDuration": "2183s",
"waitDuration": "0s",
"delayDuration": "0s",
"breakDuration": "0s",
"visitDuration": "1800s",
"totalDuration": "3983s",
"travelDistanceMeters": 19949,
"maxLoads": {
"weight": {
"amount": "3"
}
}
},
"routeCosts": {
"model.vehicles.cost_per_kilometer": 19.949,
"model.transition_attributes": 2259000.5
},
"routeTotalCost": 2259020.449
}
],
"metrics": {
"aggregatedRouteMetrics": {
"performedShipmentCount": 6,
"travelDuration": "3436s",
"waitDuration": "0s",
"delayDuration": "0s",
"breakDuration": "0s",
"visitDuration": "3600s",
"totalDuration": "7036s",
"travelDistanceMeters": 26135,
"maxLoads": {
"weight": {
"amount": "3"
}
}
},
"usedVehicleCount": 2,
"earliestVehicleStartTime": "2024-07-08T16:00:00Z",
"latestVehicleEndTime": "2024-07-08T17:06:23Z",
"totalCost": 4555027.135,
"costs": {
"model.vehicles.cost_per_kilometer": 26.135,
"model.transition_attributes": 4555001
}
}
}
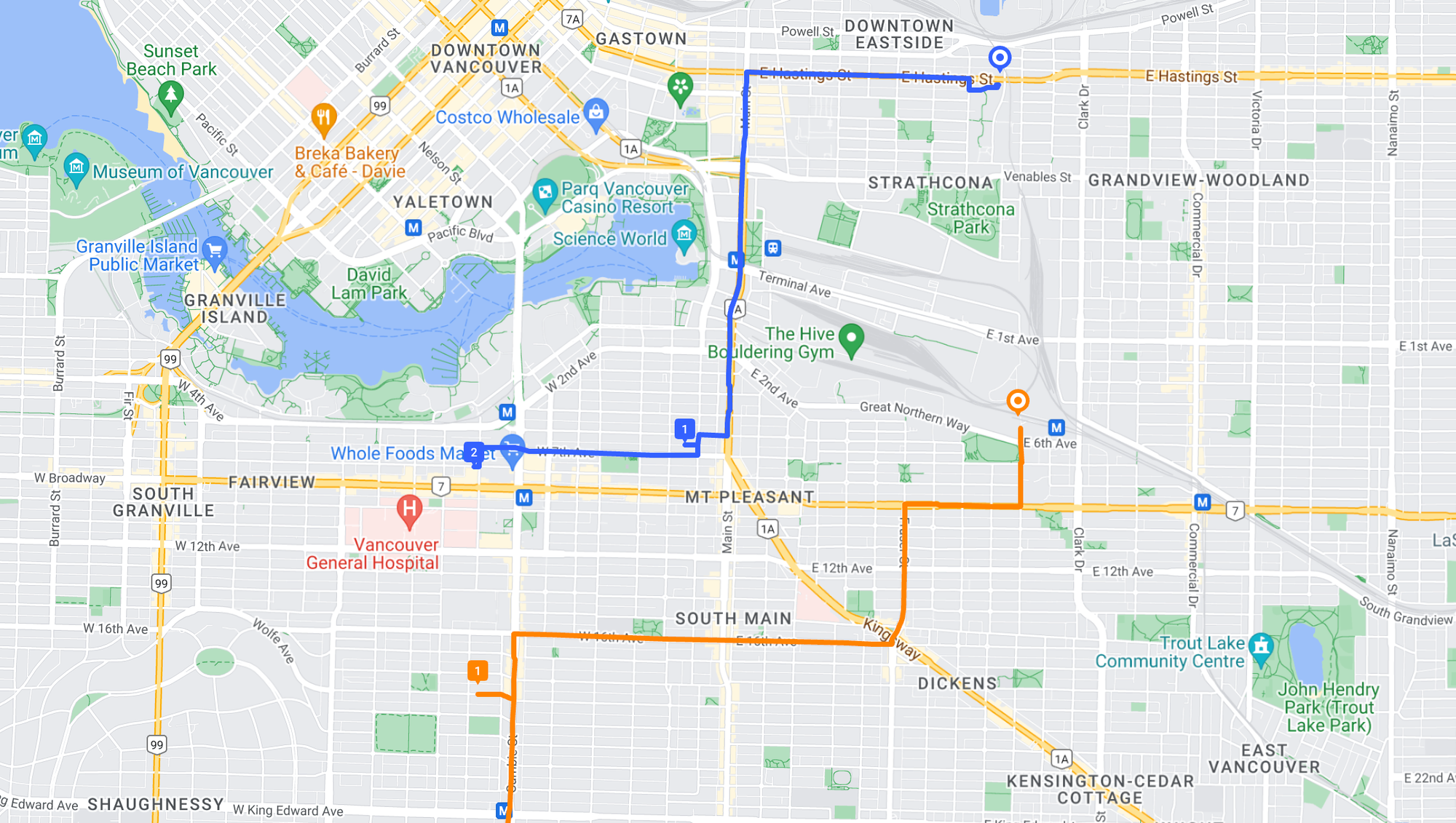
And here's what the final set of routes look like:
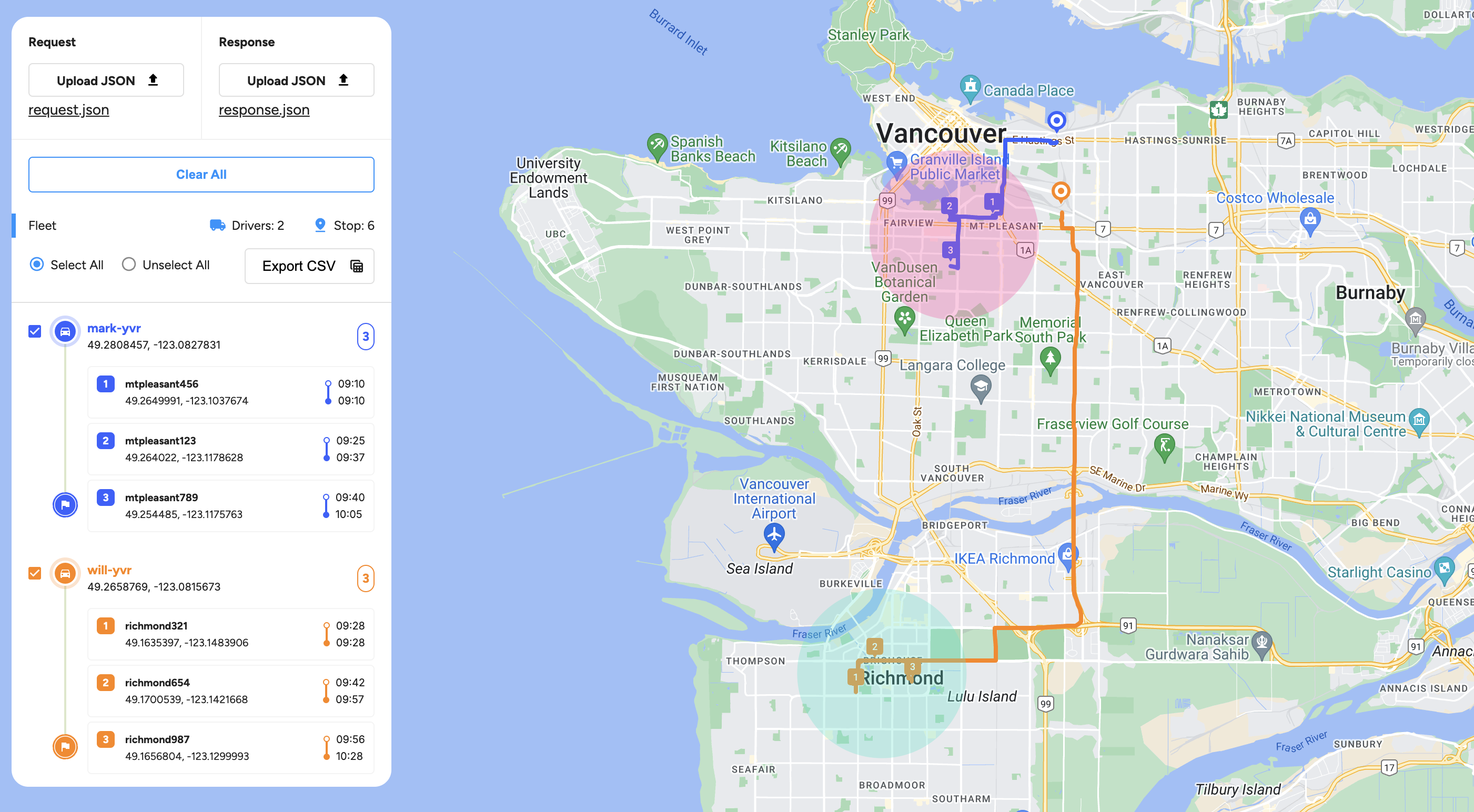
Just like we hoped, we get two perfect clusters (pink and teal) for both orange and blue drivers. `
Conclusion
Using soft constraints to cluster routes helps group stops that are geographically close together, reducing travel distances and minimizing fuel consumption, time, and operational costs. By discouraging longer trips between far-apart stops through penalties, vehicles tend to stay within tighter clusters. Most importantly, drivers and route planners vastly prefer routes that are tightly clustered together, so you are less likely to receive pushback from drivers and operations staff when implementing an automated routing system in your logistics business.
👋 As always, if you have any questions or suggestions for me, please reach out or say hello on LinkedIn.
Next: Part 8: GMPRO docs: Driver load balancing with soft constraints